poj3844水题，检查同于相同的数量即可，注意一下余数为零的情况，然后ans=西格玛c(2,n)

最近一直在搞java课程设计，一直在用java的ide，于是就悲剧了。。。

不停地TLE，时不时还来几次RE，于是我求助好友，看到他们c++的ac代码，和我差不多一样的，都过了。。。

import java.util.*;

public class Main {

    public static void main(String[] args) {
        //Scanner cin = new Scanner(System.in);

        Scanner cin = new Scanner(new BufferedInputStream(System.in));

        int a = cin.nextInt();
        for (int cas = 0; cas < a; ++cas) {

            int mod = cin.nextInt();
            int num = cin.nextInt();

            int[] sum = new int[num];

            sum[0]=cin.nextInt()%mod;
            for (int i = 1; i < num; ++i) {
                sum[i]=(sum[i-1]+cin.nextInt())%mod;
            }
            int[] count =new int[mod];
            count[0]=1;

            int ans = 0;
            for (int i = 0; i < sum.length; i++) {
                ans+=count[sum[i]];
                count[sum[i]]++;
            }

            System.out.println(ans);
        }

    }
}

这代码改成c++肯定过，可惜java超时了。

哎，人品不好

这里转发一篇《给JAVA同学刷OJ的建议》吧，以飨后人：

1. 如果时间或是空间很紧张，不要相信任何系统库。ArrayList, LinkedList, Hashtable, HashMap之类看起来很值得信任很好听的名字效率都低得可怜，不仅如此，还异常地消耗内存。这不是-O2下的vector，即便是std::map的效率都比HashMap高得多。唯一可以信赖的是数组，效率还过得去。

这里说一个小技巧，比如需要实现一个int->int的映射，可以先开一个数组，直接用mod定址，这是非常效率高的。在出现冲突时，再扔到一个HashMap里。一般来说，控制得好的话，HashMap里的总数应该不会达到总共的10%，然后整个时间和空间效率就基本可以满意了，也节约代码。

2. 语言特性和频繁地申请对象使Java不可避免地在效率上远落后于C/C++，但抛开效率，很多在C里会犯的低级错误都不会在Java里犯了，而且运行时抛出的异常有助于迅速检查代码。当测试过几个数据之后，再根据逻辑读一遍代码，就基本是通过了。通读程序很重要，有利于发现测试不易检查出的bug。

3. 如果有一个IDE将大大提高开发的效率，对于C或是C++来说，这种提高很有限，但Java的话则会很多。

4. regex效率尚可，乃一大利器，理论上说，Regional中(只要是Linux系统的Online Judge也可以)C/C++也是可以使用<regex.h>，但功能比java.util.regex里的少得多。

5. Java没有complex，给计算几何代码编写带来一些困难，但实现一个也不是非常困难。Math的功能尚可

曾经在POJ搜集的一些有趣的帖子。应Ctool兄要求转发其中一部分。我收藏夹也丢了不少，欢迎大家补充，哈哈。

求硕士博士以及同等学历者

http://poj.org/showmessage?message_id=46509

许诺：

http://poj.org/showmessage?message_id=20189

这个人要起诉北大：

http://poj.org/showmessage?message_id=66816

北航未来的女婿们：

http://poj.org/showmessage?message_id=131030

谁要写情书的，请参考这个题目

http://poj.org/problem?id=2482

狂人： 

http://poj.org/showmessage?message_id=111476

地震纪念

http://poj.org/showmessage?message_id=119531

ICPC与挂科：

http://poj.org/showmessage?message_id=87329

不明真像的群众讨论某神牛ID：

http://poj.org/showmessage?message_id=110754

传说中的神仙姐姐

http://poj.org/showmessage?message_id=57666

看到这个题目肯定有很多人感到奇怪，topcoder也能用汇编?有这种先例吗？
大家不妨看看这个链接：http://www.topcoder.com/stat?c=problem_solution&rm=300564&rd=13698&pm=10336&cr=10597114
没错。这就是Psyho在srm436中的1000pt现场代码。而下面这段就是传说中的内嵌汇编。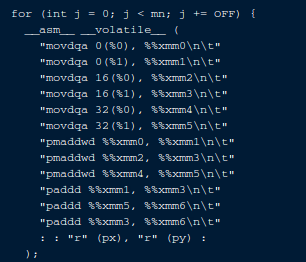


由于本篇文章主要是讨论汇编语言在topcoder里的应用，所以以内联汇编为主，不会从头来讲汇编语法。
另外，关于内联汇编的基本语法大家可以参考 Gcc嵌入式汇编和 AT&T 汇编语言与GCC 内嵌汇编简介

相信大家已经看完语法，跃跃欲试了。那么我们先该写点什么呢。果断打开POJ来A+B吧。这东东最基础了。

我相信现在大家经过折腾已经写出了最简单格式的A+B，如果还没能写出的请仔细阅读《AT&T 汇编语言与GCC 内嵌汇编简介》

那上面对于可能出现的错误讲得比较清楚。我们的第一版本的代码可能如下：

#include<stdio.h>
int main(void)
{
    int a,b;scanf("%d%d",&a,&b);
    __asm__ __volatile__ (
        "addl %1,%2 \n\t"
        :"=r"(a)
        :"r"(b),"0"(a));
    printf("%d\n",a);
    return0;
}

现在我们发现这个a在输入和输出里面都出现了，这个很不爽。现在有一个比"="更爽的限制符"+"，可以表示读写型的。修改的代码如下：

#include<stdio.h>
int main(void)
{
    int a,b;scanf("%d%d",&a,&b);
    __asm__ __volatile__ (
        "addl %1,%0 \n\t"
        :"+r"(a)
        :"r"(b));
    printf("%d\n",a);
    return0;
}

这个代码看起来比较满意了。不过写%0,%1这些东西总有些小不爽，所以新版的gcc又添加了一种新的写法：

#include<stdio.h>
int main(void)
{
    int a,b;scanf("%d%d",&a,&b);
    __asm__ __volatile__ (
        "addl %[b],%[a] \n\t"
        :[a]"+r"(a)
        :[b]"r"(b));
    printf("%d\n",a);
    return0;
}

        至此，我们A+B算是折腾完了。现在简单总结一下，嵌入汇编的结构虽然看起来复杂，实际上我们发现只要写对了输入输出，那么其他的东东，我们只要写一行行的汇编语句就行了。这个比起写纯汇编可爽多了啊。而且通常来讲，循环的迭代部分是不怎么耗损时间的，真正麻烦的是里面的处理代码。所以我们基本不需要用汇编写循环了，只要把循环内的关键部分改成汇编就好了。

        现在我们的问题又来了，第一，真的这么简单吗？好像不是，我们写代码来提高效率需要大量运用寄存器，我们这样把eax,ebx等等寄存器改来改去太危险了。第二，就算我们汇编熟练了，那么这样又能提高多少的效率啊，好像也不大吧。

        不得不承认上面的担心是有道理的。但是我们再认真读读s436的1000pt。我们发现这个题目的暴力算法复杂度是3.6*10^9。以我们的经验来讲，topcoder的机器搞搞10^8复杂度的乘法还是OK的，但是10^9注定悲剧啊。难道汇编真有这么神奇的力量？我们现在仔细看看Psyho的代码，我们发现根本没有我们熟悉的eax,ebx等等，反而是一些xmm0,xmm1之类的。对了，这个就是关键所在了。这个是SSE2(Streaming SIMD Extensions 2，Intel官方称为SIMD 流技术扩展2）的东东，简单来说，xmm0是128位的寄存器。也就是说：第一，我们担心的eax,ebx已经是浮云啦；第二，效率最差我们可以让它提高4倍，因为我们用的是128位寄存器。

         尽管如此，那么我们就真的可以解决3.6*10^9的复杂度吗？其实强大的SSE2还有新的强大指令集啦。我们搜一下pmaddwd，这个居然就是压缩乘法与加法指令，而且题目给我们的数据都是%100,也就是short存足够了。那这样。。。无敌啦。完美啦。我们的乘法和加法只需要一个指令，而且我们处理起来是128位一搞，而且Psyho的代码中三个pmaddwd和paddd由于是完全独立的，我们可以认为存在多路并发处理的机会。我们再看看OFF,一次就跳过了24，这样的优化足够了。

        当然Psyho的代码优化还不止如此，我们注意到声明部分的__attribute__((aligned(16)))，我们可以知道，他采用对齐优化了加载内存的速度，而movdqa就是用于一次加载对齐的128位的指令。所以由于对齐的声明他的代码外层循环需要步长为8。（128位，short为16位，8==128/16）

        经过测试其实该题不需要采用对齐来优化就可以过了，没有对齐的情况下，逻辑极其简单，关键代码可以精简如下：

short x[63000],y[130000];
classCircularShifts{
public:
    int maxScore(int,int,int,int,int);
};
intCircularShifts::maxScore(int n,int _Z0,int _A,int _B,int _M){
    LL Z0=_Z0, A=_A, B=_B, M=_M;
    VC < LL > z;
    z.PB(Z0 % M);
    REP(i, n+n-1) z.PB((z[i]* A+B)% M);
    REP(i, n) x[i]= z[i]%100,y[n+i]=y[i]= z[i + n]%100;
    int mx =0;
    #define OFF 24
    REP(i,n){
      intno=0,mn=n-n%OFF;
      short*ed=x+mn;
      int vt[4]={0};
      __asm__ __volatile__ (
        "xorpd %%xmm6, %%xmm6\n\t"
        :::
      );
      for(short*px=x,*py=y+i; px != ed; px+= OFF,py+=OFF){
        __asm__ __volatile__ (
          "movdqu 0(%1), %%xmm1\n\t"
          "movdqu 16(%1), %%xmm3\n\t"
          "movdqu 32(%1), %%xmm5\n\t"
          "pmaddwd 0(%0), %%xmm1\n\t"
          "pmaddwd 16(%0), %%xmm3\n\t"
          "pmaddwd 32(%0), %%xmm5\n\t"
          "paddd %%xmm1, %%xmm3\n\t"
          "paddd %%xmm5, %%xmm6\n\t"
          "paddd %%xmm3, %%xmm6\n\t"
          ::"r"(px),"r"(py):
        );
      }
       __asm__ __volatile__ (
                "movdqu %%xmm6, %0\n"
                :"=m"(*vt)::
            );
      no= vt[0]+ vt[1]+ vt[2]+ vt[3];
      FOR(j, mn, n)no+= x[j]* y[i + j];
      mx=max(mx,no);
    }
  return mx;
}

      当然，对齐是个好习惯，这个题目对齐与不对齐耗时差距近0.5s。另外可能有人会问，除了这种有好的SSE指令这种情况下，其他情况也能有很爽的优化吗？最常用的肯定是位操作了，现在我们有了128位的寄存器，位操作的效率就提高很多了。关于位操作优化的效果，可以参见Rizvanov_de_xXx提交的srm 494 practice room 1000pt。

      最后做个最简单的总结，根据这两份代码我们可以发现尽量采用指针，最后的结果movdqu回去就行了，计算都在xmm0，xmm1这些寄存器里面做，一次能搞128位。最后我们达到的效果就是即便10^9的复杂度，我们的暴力算法也有希望了。

      本篇文章在简单介绍内嵌汇编后，主要是针对SSE的指令和寄存器来介绍汇编的优化。最终我们绕过eax,ebx这些易错的寄存器，反而还取得了一次解决128位的效果，达到了高度优化和编程简单。由于篇幅有限，本文未详细介绍汇编语言和内联汇编的知识，希望文章开头给出的链接有所帮助，另外对于C语言一些能更好生成目标代码的编写技巧，也没有讨论，这个部分大家可以参见骆可强的国家集训队论文《论程序底层优化的一些方法与技巧》。

参考文献：

GCC Extended-Asm http://gcc.gnu.org/onlinedocs/gcc/Extended-Asm.html

Linux内核完全剖析 赵炯

GCC嵌入式汇编 http://oss.org.cn/kernel-book/ch02/2.6.3.htm

AT&T 汇编语言与GCC 内嵌汇编简介 chforest_chang@hotmail.com

论程序底层优化的一些方法与技巧 骆可强

http://poj.org/problem?id=3543

题意是给黑、白砖块的数量，组成国际象棋棋盘那样黑白相间正方形，求最大变长。

这题看了解题报告再做就没意思了，建议先自己试试，不难的：

以下剧透，慎入：

看过题目就知道是一道大水题，但Total Submissions: 2130 Accepted: 919只是个小水题，

本题的特殊情况有：

1)黑色和白色的砖的个数都为0，输出impossible

2)黑色或白色的砖的个数为1，或者两者个数都为1，输出1；

剩下的就是取a,b最小值乘以二加一再开方取整输出了，但如果a==b乘以二之后不用加一，我在这里WA了

此外，题目给1000ms，status里有不少0ms，但是java的最快6422MS,我不幸以8000+ac，同时贡献了3个wa（不够细心）  1个re（莫名其妙）  2个ce（拜默认g++所赐）

哈哈，最近状态不好，写出来发泄之！